Function
- A program segment that carries out some specific,well-defined task.
- Example
- A function to add two numbers
- A function to find the largest of n numbers
- A function will carry out its intended task whenever it is called or invoked
- It Can be called multiple times.
- Every C program consists of one or more functions
- One of these functions must be called main
- Execution of the program always begins by carrying out the instructions in main
- Functions call other functions as instructions
- Function Control Flow
- Calling function (callee) may pass information to the called function (callee) as parameters/arguments For example, the numbers to add
- The callee may return a single value to the caller

-
Some functions may not return anything
Details of Terms used in function


Another Example


Why We Use Functions?
- Allows one to develop a program in a modular fashion
- Divide-and-conquer approach
- Construct a program from small pieces or components
- Use existing functions as building blocks for new programs
- Abstraction: hide internal details (library functions)
Scope of a variable in Functions
- Part of the program from which the value of the variable can be used (seen)
- Scope of a variable - Within the block in which the variable is defined
- Block = group of statements enclosed within { }
- Local variable =scope is usually the function in which it is defined
- So two local variables of two functions can have the same name, but they are different variables
- Global variables =declared outside all functions (even main)
- scope is entire program by default, but can be hidden in a block if local variable of same name defined

Calling Convention
- It Called by specifying the function name and parameters in an instruction in the calling function.
- When a function is called from some other function, the corresponding arguments in the function call are called actual arguments or actual parameters
- The function call must include a matching actual parameter for each formal parameter
- Position of an actual parameters in the parameter list in the call must match the position of the corresponding formal parameter in the function definition
- The formal and actual arguments must match in their data types


Points to note
- The identifiers used as formal parameters are "local".
- It is not recognized outside the function
- Names of formal and actual arguments may differ
- A value-returning function is called by including it in an expression
- A function with return type T ( not void) can be used anywhere an expression of type T can be used.
- Returning control back to the caller
- If nothing returned
- return;
- or,until reaches the last right brace ending the function body.
- If something returned
-
return expression;
Advanced Features of Functions
We will see the advanced some features of functions are given below:-
Function Declaration and Prototypes
- Usually, a function is defined before it is called
- main() is the last function in the program written
- Easy for the compiler to identify function definitions in a single scan through the file
- However, many programmers prefer a top-down approach, where the functions are written after main()
- Must be some way to tell the compiler
- Function prototypes are used for this purpose
- Only needed if function definition comes after use
- Function prototypes are usually written at the beginning of a program, ahead of any functions(including main())
- Prototypes can specify parameter names or just types (more common)
- Examples:
- int gcd (int , int );
- void div7 (int number);
- Note: the semicolon at the end of the line.
- The parameter name, if specifed, can be anything; but it is a good practice to use the same names as in the function definition
Some more points
- A function cannot be defined within another function
- All function definitions must be disjoint
- Nested function calls are allowed
- A calls B, B calls C, C calls D, etc.
- The function called last will be the first to return
- A function can also call itself, either directly or in a cycle
- A calls B, B calls C, C calls back A Called recursive call or recursion
Example:main calls ncr, ncr calls fact
int ncr (int n, int r);
int fact (int n);
void main()
{
int i, m, n, sum=0;
scanf ("%d %d", &m, &n);
for (i=1; i <=m; i+=2)
sum = sum + ncr (n, i);
printf ("Result: %d \n",sum);
}
//ncr function definition
int ncr (int n, int r)
{
return (fact(n) / fact(r) / fact(n-r));
}
//fact function declaration
int fact (int n)
{
int i,temp=1;
for (i=1; i<=n; i++)
temp *= i;
return (temp);
}
Call by Value and Call by Reference
It is used when invoking functions:
Call by value
- Passes the value of the argument to the function
- Execution of the function does not change the actual parameters
- All changes to a parameter done inside the function are done on a copy of the actual parameter
- The copy is removed when the function returns to the caller
- The value of the actual parameter in the caller is not affected
Avoids accidental changes
Call by reference
- Passes the address to the original argument.
- Execution of the function may affect the original
- Not directly supported in C except for arrays
library Functions
- Set of functions already written for you,and bundled in a "library"
- C library provides a large number of functions for many things
- We look at functions for mathematical use.
- Math library functions
- perform common mathematical calculations
- Must include a special header file
- Example
- printf("%f", sqrt(900.0));
- Calls function sqrt, which returns the square root of its argument
- Return values of math functions can be float/double/long double
- Arguments may be constants, variables, or expressions
-
Example:printf, scanf, getchar etc.
Math library Functions
-
#include < math.h >
| Function | Working of function |
|---|---|
| double acos(double x) | Compute arc cosine of x. |
| double asin(double x) | Compute arc sine of x. |
| double atan(double x) | Compute arc tangent of x. |
| double atan2(double y, double x) | Compute arc tangent of y/x. |
| double cos(double x) | Compute cosine of angle in radians. |
| double cosh(double x) | Compute the hyperbolic cosine of x. |
| double sin(double x) | Compute sine of angle in radians. |
| double sinh(double x) | Compute the hyperbolic sine of x. |
| double tan(double x) | Compute tangent of angle in radians. |
| double tanh(double x) | Compute the hyperbolic tangent of x. |
| double ceil(double x) | Get smallest integral value that exceeds x. |
| double floor(double x) | Get largest integral value less than x. |
| double exp(double x) | Compute exponential of x. |
| double fabs (double x) | Compute absolute value of x. |
| double log(double x) | Compute log to the base e of x. |
| double log10 (double x) | Compute log to the base 10 of x. |
| double pow (double x, double y) | Compute x raised to the power y. |
| double sqrt(double x) | Compute the square root of x. |
Introduction to Pointers
- It is powerful,but difficult to master.
- It simulate call-by-reference.
- It is closely related with arrays and strings
Pointer Variable Definitions and Initialization
- Pointer variables
- Contain memory addresses as their values
- Normal variables contain a specific value (direct reference) count
- Pointer is a variable that contains address of a another variable that has a specific value (indirect reference)
- Indirection – referencing a pointer value
- Pointer definition
- * used with pointer variables
- int *myPtr;
- Defines a pointer to an int (pointer of type int *)
- Multiple pointers require using a * before each variable definition
- int *myPtr1, *myPtr2;
- It can define pointers to any data type
- Initialize pointers to NulL or an address
Pointer Notation
- & (address operator)
- It returns address of operand
Back to Function Calls
A callback is any executable code that is passed as an argument to
other code, which is expected to call back (execute) the argument at a
given time. In simple language, If a reference of a function is passed
to another function as an argument to call it, then it will be called
as a Callback function. In C, a callback function is a function that
is called through a function pointer.
Below is a simple example in C to illustrate the above definition to
make it more clear:
// A simple C program to demonstrate callback
#include <stdio.h >
void Ask()
{
printf("I am function Ask\n");
}
// callback function
void Blow(void (*ptr)())
{
(*ptr) (); // callback to Ask
}
int main()
{
void (*ptr)() = &A;
// calling function Blow and passing
// address of the function Ask as argument
Blow(ptr);
return 0;
}
Conclusions
(a)If we want that the value of an actual argument should not
get changed in the function being called, pass the actual argument by
value.
(b)If we want that the value of an actual argument should get
changed in the function being called, pass the actual argument by
reference.
(c)If a function is to be made to return more than one value at
a time then return these values indirectly by using a call by
reference.
Recursion
The Recursive function is a function that calls itself to solve the problem.
When should we use recursion?
If any problem can be divided into multiple smaller version of the same problem, we can use Recursive approach to solve that problem.
Calculate the factorial of a given number. fact(3) = 6 (3 * 2 * 1) This problem can be divided into three smaller versions. Declare fact = 1 1. fact = fact * 3 2. fact = fact * 2 1. fact = fact * 1
Basic Rules of Recursion
1. The recursive function should call itself.
2. The recursive function should have an ending point where it doesn't make further recursive calls. Also called as the base case. Base case will not need any recursive call to solve.
Example Base cases
Factorial of 0 is 1 and 1 is 1.
Fibonacci of 0 is 0 and 1 is 1.
The above cases are straightforward and those cases don't need any
recursive call.
3. All the recursive calls should align towards the base case.
Example
When calculating factorial(5). Here, base case is factorial(0) = 1 ||
factorial(1) = 1.
Recursive functions should go like factorial(5),
factorial(4),factorial(3),factorial(2), finally ends with factorial(1)
or factorial(0).
If it goes in another way like factorial(6)....factorial(100) etc. The
recursion won't end.
Let's solve the factorial problem using recursion
Algorithm
1.Find the base case. factorial(0) = 1 || factorial(1) = 1.
2. Write the factorial function and call itself recursively untill it
meets the base case.
3. Calculate and return the answer.
int factorial(int n)
{
//base case fact(0) = fact(1) = 1
if(n <= 1)
return 1;
//calculate the factorial
//recursively the call the above function
return n * factorial(n - 1);
}
Factorial using Recursion
#include <stdio.h>
int fact(int n)
{
if(n <= 1)
return 1;
return n * fact(n-1);
}
int main()
{
int n;
scanf("%d",&n);
if(n >= 0)
printf("%d\n",fact(n));
return 0;
}
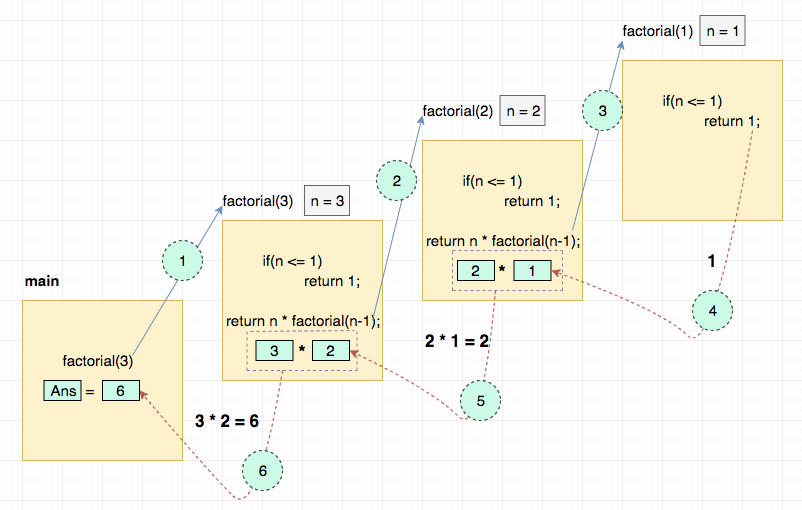
Visualizing the above recursive function
The best way of understanding the recursion is by visualizing it.
Let's understand how factorial(3) works.
Stack Overflow in Recursion
In recursion, the new function call will be created in stack memory
section.
If our recursive function doesn't have any base case or the recursive
function call doesn't align towards the base case, it will keep on
create function calls in the stack memory section.
At some point in time, the recursive function call overflows the stack
memory section as it doesn't have any stopping point.
This is also called as the stack overflow in recursion.
Recursive function won't have any base case - Stack Overflow
#include<stdio.h1>
int fact(int n)
{
return n * fact(n-1);
}
int main()
{
int n;
scanf("%d",&n);
if(n >= 0)
printf("%d\n",fact(n));
return 0;
}
The above recursive function doesn't have any base case.
If the given input is 3, the recursive calls will be fact(2), fact(1),
fact(0), fact(-1),.... and so on. It will never end.
This will overflows the stack memory section.
Chapter 6 Quiz
#include< stdio.h >
int fun(int n)
{
if (n==4)
return n;
else
return 2*fun(n+1);
}
int main()
{
printf("%d",fun(2));
return 0;
}
int f(int n)
{
static int i = 1;
if(n>=5) return n;
n = n+1;
i++;
return f(n);
}
The value returned by f(1) is
 CHAPTER 6
CHAPTER 6


